6. Understanding Option Greeks

Option Greeks are essential for understanding how and why an option’s price moves. They are like the diagnostics of an option, telling you its sensitivity to various factors. There are five primary Greeks: Delta, Gamma, Theta, Vega, Rho. Don’t be intimidated by the Greek letters – we’ll break each down in simple terms with examples, focusing on intuition more than math.

Delta (Δ):

Delta measures how much an option’s price is expected to change if the underlying price changes by 1 unit. In simpler terms, delta is the option’s sensitivity to the stock/index price.

• For a Call option, delta is positive (between 0 and 1). Example: A NIFTY call with delta 0.5 means if NIFTY goes up 100 points, the call’s price will increase by about 50 points (0.5 * 100). If NIFTY falls 100, the call’s price drops ~50. Higher delta (closer to 1) means the option moves almost like the underlying. ITM calls have delta approaching 1, ATM call ~0.5, deep OTM call might be 0.1 (hardly moves unless Nifty moves a lot).

• For a Put option, delta is negative (between 0 and -1) because puts move opposite the underlying. A put with delta -0.5 will gain 50 if the index falls 100, and lose 50 if the index rises 100 (which makes sense: put up when underlying down). Deep ITM puts have delta ~ -1, ATM put ~ -0.5, far OTM put ~ -0.1.

Delta also has another interpretation: roughly, probability of expiring ITM. For example, an ATM call with delta 0.5 is often said to have ~50% chance to end ITM, a deep OTM call with delta 0.1 might have ~10% chance. This isn’t a hard rule, but a useful intuition. Traders use delta for hedging: e.g., if you sell a call with delta 0.5, you can hedge by buying 0.5 units of the underlying to be delta-neutral

Gamma (Γ):

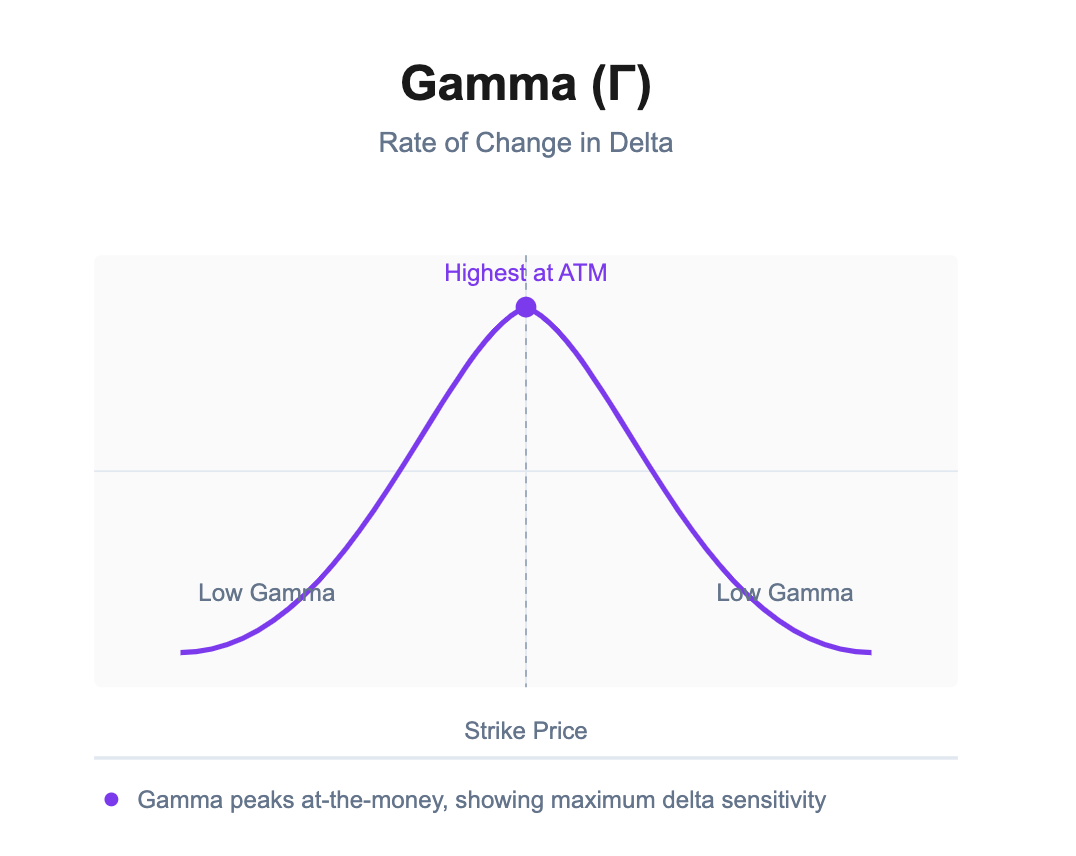
Gamma measures the rate of change of Delta with respect to underlying price changes. In other words, gamma shows how curved the option’s response is. If delta is how much you move, gamma is how much that movement itself can change.

• High gamma means delta can change quickly – the option is very sensitive to even small moves and its behavior (delta) will swing. Low gamma means delta is relatively stable.

  

• ATM options (especially near expiry) have the highest gamma. This is why a near-expiry ATM option is volatile: a small move in underlying can suddenly turn it from ATM to ITM or OTM, swinging delta from 0.5 to 1 or to 0, which makes the price jump or crash

  

• Deep ITM or deep OTM options have low gamma (their delta is near constant: deep ITM call delta ~1 always, deep OTM call delta ~0).

• Example: Suppose a BankNifty 40,000 call has delta 0.5 and a high gamma of 0.2. If BankNifty moves up 100 points, the call’s delta might increase by 0.2*100 = 20 points (not exactly linear, but conceptually). So delta goes from 0.5 to 0.7, meaning the call becomes more sensitive going forward.

For risk management, gamma is important: if you’ve sold options, high gamma means you can get into trouble fast with a quick move (because your position’s delta could go from small to large, meaning your exposure explodes).

Theta (Θ):

Theta measures the time decay of an option – how much value the option loses per day as expiration approaches, all else equal. Theta is usually expressed as a negative number for long options (because each day, long options lose value).

• For instance, a NIFTY option might have Theta = -5 (meaning it loses ₹5 in premium per day). If two days pass with nothing happening, expect ~₹10 drop in that option’s price due to time decay.

  

• ATM options often have higher absolute theta than far OTM or deep ITM (because they have more extrinsic value to decay). Also, theta accelerates as expiry nears; an option 2 months out might lose little per day, but in the last week, the decay is much sharper.

• Sellers love positive theta (they earn the decay). Buyers suffer theta (the clock is ticking).

• Weekend effect: Note that in India, often Thursday evening to Friday, after expiry, next week’s options might already reflect 2 days of decay (Saturday and Sunday) being priced out. So Monday open sometimes has a decay jump as well (though markets often anticipate it by Friday).

Vega (ν):

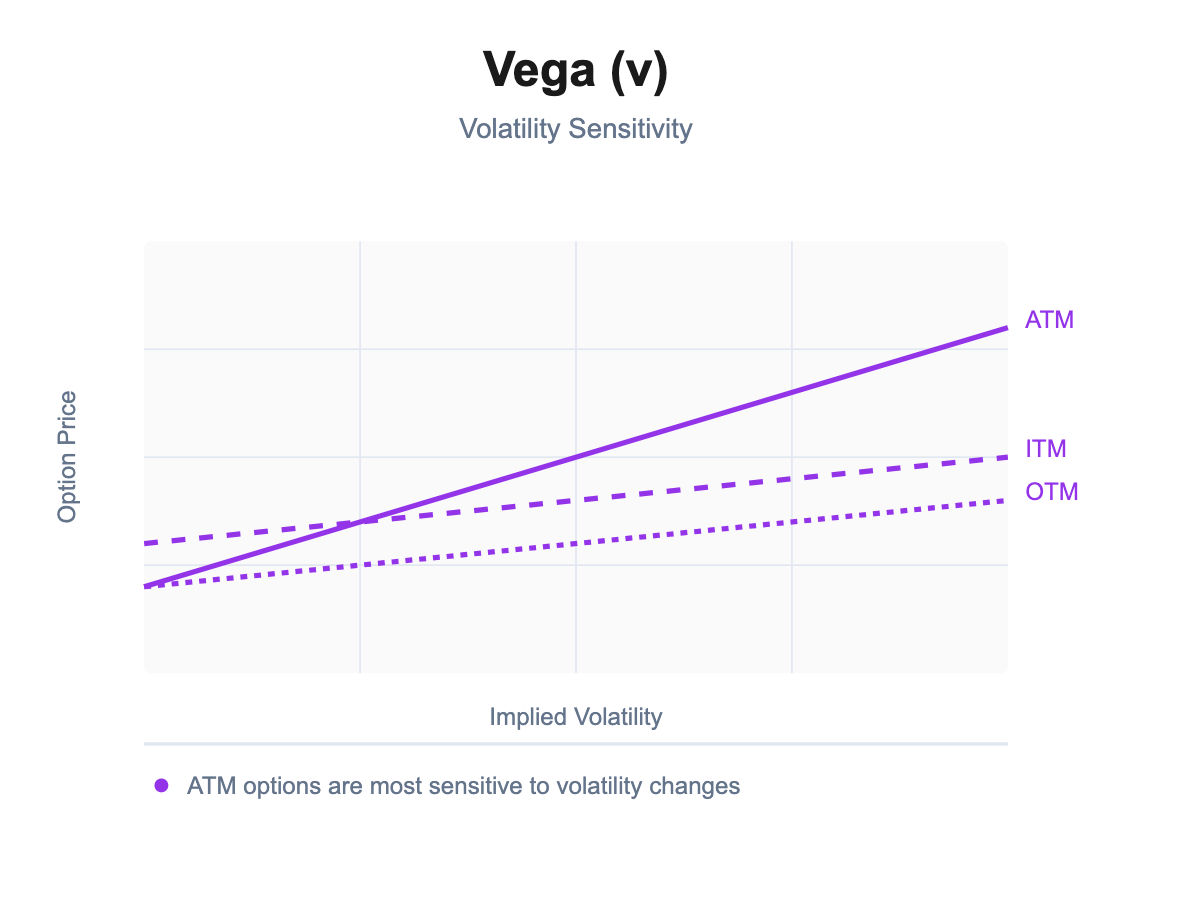
Vega (not actually a Greek letter, but we call it one) measures the option’s sensitivity to volatility. Specifically, how much the option’s price will change for a 1 percentage point change in Implied Volatility (IV).

• If an option has vega 0.2, and IV goes up from 15% to 16%, the option’s price will increase by 0.2 (all else equal). If IV drops, option price drops by that amount.

• Vega is higher for options with more time to expiry (because volatility has more time to act) and for ATM options (which are most impacted by changes in IV). Near-expiry options have low vega (they're mostly about intrinsic at the end)

  

• Implied Volatility is basically the expected volatility baked into the option price. We’ll talk more about it next section. But vega is why around big events (when IV jumps), even if the underlying doesn’t move, option prices can rise – and after the event, as IV falls (IV crush), option prices fall. Vega quantifies that effect.

• Example: Suppose there’s an RBI policy announcement in a few days. Nifty ATM options’ IV goes up; an option with vega 0.15 might gain ₹0.15 for every 1% rise in IV. If IV jumps 5 points (say 15% to 20%), that’s about ₹0.75 added from volatility alone (on top of any intrinsic changes).

Rho (ρ):

Rho measures sensitivity to interest rates (specifically, a 1% change in risk-free interest rate). It’s the most abstract for many traders and often the least impactful for short-dated options.

• For calls, rho is positive (higher rates slightly increase call value), and for puts, rho is negative (higher rates slightly decrease put value). This is because if interest rates are high, the cost of carrying a long position in the underlying is higher, which makes calls a bit more valuable relative to just holding the stock.

• In practice, in India’s context, interest rates don’t change dramatically in the short term, and most traders ignore rho for near-term options. It matters more for longer-term options (LEAPS) or when interest rates are moving significantly

  

• You likely won’t feel rho’s effect in day-to-day trading. For example, if RBI suddenly cut rates by 1%, your long calls might lose a little value (rho effect), and long puts gain a bit – but often this is overshadowed by the market’s reaction to the rate cut itself (which will move underlying and IV). So rho often gets lost in the noise.

Greeks in Practice:

Each Greek isolates one factor, but in reality they all act together. When NIFTY moves, your option’s delta and possibly gamma are in play; as time passes, theta chips away; as volatility changes, vega adds or subtracts. Understanding Greeks helps in strategy:

• Risk Management: If you sold options, you might be concerned about gamma risk (big moves) and vega risk (if volatility spikes against you). You might choose strikes or time frames to manage that (e.g., avoid selling too close to expiry if you fear gamma).

• Hedging: Delta can be hedged by underlying. Vega can be hedged by trading other options (like a spread). Market makers and advanced traders actively manage Greeks to keep their overall portfolio risk in check.

• Choosing Options: If you want a pure directional bet for a short time, you may prefer an option with a certain delta and high gamma (to get a quick payout on a move) but realize it comes with theta decay and vega exposure. If you want to avoid time decay as much, maybe go further ITM (higher intrinsic, lower theta percent-wise).

Quick recap of Greeks in a handy way:

• Delta: Directional exposure (how option moves with underlying). Think “if underlying moves, my option...”.

• Gamma: Stability of that exposure (will my option’s behavior change quickly?).

• Theta: Time decay (how much do I pay for waiting?).

• Vega: Volatility sensitivity (I care about event/no-event volatility swings).

• Rho: Interest rate sensitivity (usually minor for us).

Whew, that’s a lot of theory – but with this understanding, we can now better grasp how volatility plays into option pricing, which is our next topic, and one of the most important aspects of options trading.